Radar Meteorology 1: Fundamentals of weather radar measurement
Notes of Fabry, F. (2018). Radar meteorology: principles and practice. Cambridge University Press. Ch. 2
What is radar?
Radar (RAdio Detection And Ranging) is an active remote sensor that emits strong signals at radio or microwave frequencies and receive the reflections of targets.
What does a radar do?
- Generate a strong signal by radar transmitter.
- Focus the signal in a specific direction along which locate the targets. This is the role of the antenna.
- Receive the (very) faint echoes from the targets, the intensity of the returned signal being a tiny fraction of what was emitted. This is done by the combination of the antenna and the radar receiver.
- Extract raw data from the received signals (target range, echo strength, velocity,…) by the signal processor.
- The radar product generation hardware and software then shifting the raw data to meteorological information
- The radar product display system displays and disseminates the information.
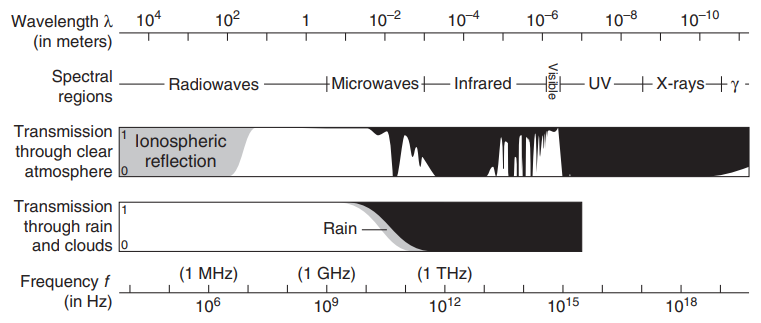
Microwaves and the atmosphere
The radio wave and microwave atmospheric window
The transparency of the atmosphere to EM waves depends critically on the wavelength of those waves.
atmospheric window: the limited region of the EM spectrum to which the atmosphere is transparent.
Scattering regimes
Scatter can be defined as the re-radiation of the incident radiation of particles or objects called scatterers. Partial reflections occur when EM waves propagating in the medium with refractive index $n_1$ meet another medium with refractive index $n_2$.
In the atmosphere, scatterers vary considerably in size, ranging from gas molecules (~$10^{-10}$ m) to layers of air at different temperatures and humidity (several meters). Scatterers will interact differently with radiation depending on their sizes and the wavelength of the incoming EM waves.
Objects with sharp boundaries
Volume scattering coefficient $\beta$. In the absence of attenuation, the change in flux of energy $E$ at wavelength $\lambda$ due to scattering is given by
\[\frac{\mathrm{d}E(\lambda)}{E(\lambda)}=-\beta\mathrm{d}s\]For spherical scatterers of diameter D in a medium with unit refractive index, the volume scattering coefficient is given by
\[\beta=\frac{\pi}{4}\int_{0}^{\infty}N(D)D^2\xi_\mathrm{s}(n(\lambda),D,\lambda)\mathrm{d}D\]where $N(D)$ is the number concentration of particles with diameter $D$ and $\xi_\mathrm{s}(n(\lambda),D,\lambda)$ is the scattering efficiency factor , with $n(\lambda)$ being the complex refractive index of the scatterer. Scattering intensity is hence a function of the cross-sectional area of bodies on the path of the radar beam ($\int N(D)D^2\pi/4\mathrm dD$), and how efficiency these bodies scatters radiation given its size and refractive index.
Size parameter $\gamma$ (ratio of circumference of the scatterer and the wavelength):
\[\gamma=\frac{\pi D}{\lambda}\]For $\vert n(\lambda)\gamma\vert<1$ (scatterers much smaller than the wavelength, Rayleigh scattering),
$$ \xi_\mathrm{s}(n(\lambda),D,\lambda)=\frac{8}{3}\gamma^4\left\vert\frac{n^2(\lambda)-1}{n^2(\lambda)+2}\right\vert^2
$$ therefore,
\[\beta=\frac{2\pi^5}{3\lambda^4}\left\vert\frac{n^2(\lambda)-1}{n^2(\lambda)+2}\right\vert^2\int_{0}^{\infty}N(D)D^6\mathrm{d}D\]Barring major changes in $n(\lambda)$,
\[\beta\propto\frac{D^6}{\lambda^4}\]At visible wavelengths (blue),air molecules are much smaller than $\lambda$. Hence these molecules scatter shorter wavelengths (blue) much better than longer ones (red), leading to the blue sky. At radar wavelengths ($\lambda$ often on the order of several centimeters), most atmospheric targets behave as Rayleigh scatterers. Therefore, radars using shorter wavelengths will see increased scattering from precipitation.
For scatterers much larger than the wavelength, $\xi_\mathrm{s}(n(\lambda),D,\lambda)$ depends only on the refractive index $n(\lambda)$, $\beta\propto\mathrm{cross-section\ area}$, resulting in white clouds (optical or nonselective region).
Between the two regimes is the Mie or the resonance region.
Radar reflectivity $\eta$ tht sums $\sigma_\mathrm{b}$ pre unit volume:
\[\eta=\int_0^{\infty}N(\sigma_\mathrm{b})\sigma_\mathrm{b}\mathrm{d}\sigma_\mathrm{b}=\frac{\pi^5}{\lambda^4}\left\vert\frac{n^2(\lambda)-1}{n^2(\lambda)+2}\right\vert^2\int_{0}^{\infty}N(D)D^6\mathrm{d}D\]and
\[\eta=\int_0^{\infty}N(\sigma_\mathrm{b})\sigma_\mathrm{b}\mathrm{d}\sigma_\mathrm{b}=\frac{\pi}{4}\left\vert\frac{n(\lambda)-1}{n(\lambda)+1}\right\vert^2\int_{0}^{\infty}N(D)D^2\mathrm{d}D\]for the Rayleigh and optical regimes, respectively.
Fuzzy refractive index transitions
Types of radars
Naming conventions of radar bands
Propagation in the atmosphere
Refraction
Attenuation
Basic radar measurement
Timing, range, and radial velocity
Radar returns from a distributed target
Weather surveillance
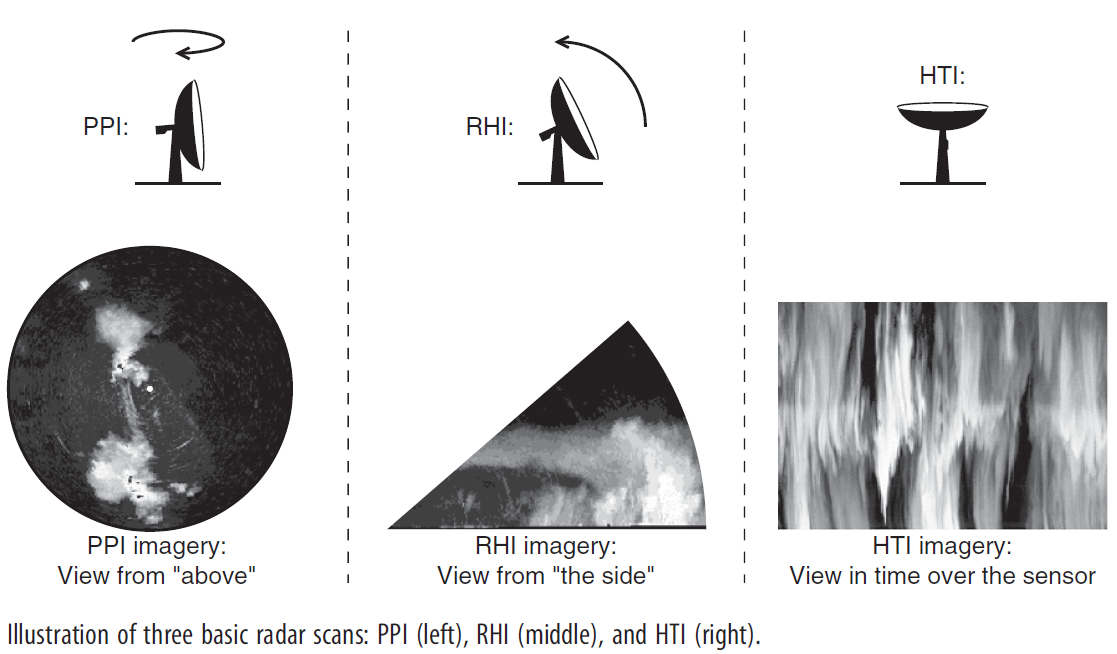
PPI: plan position indicators. The antenna scans in azimuth at a fixed elevation.
RHI: range-height indicators. The antenna scans in elevation at a fixed azimuth.
HTI: When the elevation is the zenith or nadir, range-height indicators are also called height-time indicators.